



Nächste Seite: Der Abstand
Aufwärts: Spiegelung der Vektoren
Vorherige Seite: Spiegelung der Vektoren
Inhalt
Index
Die Matrix ist ein Gebilde, die in der dualen Physik
die Komponenten der Tensoren darstellt.
Durch das Vertauschen von Zeilen und Spalten einer Matrix erhalten wir
eine neue Matrix, die transponierte Matrix
genannt wird. die transponierte
Form können wir auch aus der Spiegelung der dreidimensionalen Vektoren
gewinnen.
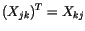 |
|
|
(2.14) |
Allgemein können wir sagen: zu jeder Matrix existiert eine
transponierte Matrix, so daß ihr Eigenprodukt oder ihr Quadrat wiederum
eine skalare bzw. invariante Matrix ergibt. Das Resultat des Produkts
zweier unterschiedlicher Matrixen ist eine Zusammensetzung der Komponenten
einer neuen Matrix bestehend aus dem skalaren Produkt der
Vierervektoren und dem Vierervektorprodukt (die Vektorverschiebungen
und das Vektorprodukt). das letztere erweist sich im allgemeinen als
unvertauschbar. Folglich ist das Produkt zweier Vierertensoren nicht
Kommutativ.
Mit anderen Worten: das Produkt zweier Vierertensoren ist von ihrer Reihenfolge
abhängig.
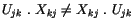 |
|
|
(2.15) |
Nach dieser Definition bilden wir nun das erste Tensorprodukt
und ermitteln das Quadrat des Tensors 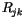 . Das
Ergebnis dieses Produkts wie schon oben angedeutet, ist ein
skalares Tensor. Die skalaren Vierertensoren werden durch die
Buchstaben mit der oberen und unteren Indizes gekennzeichnet (gemischte
Darstellung), denen eine besondere Bedeutung beigemessen wird.
. Das
Ergebnis dieses Produkts wie schon oben angedeutet, ist ein
skalares Tensor. Die skalaren Vierertensoren werden durch die
Buchstaben mit der oberen und unteren Indizes gekennzeichnet (gemischte
Darstellung), denen eine besondere Bedeutung beigemessen wird.
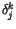 ist ein antisymetrischer
Tensor d.h. bei Vertauschen des oberen und unteren Indizes ändert er sein
Vorzeichen.
ist ein antisymetrischer
Tensor d.h. bei Vertauschen des oberen und unteren Indizes ändert er sein
Vorzeichen.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ R_{jk} \ . \ R_{kj} = \delta_j^k \ . \ (R_j)^2 \ \ , \ \ \delta_j^k = die \ \ Einheitstensor \ $}$](IMG50.GIF) |
|
|
(2.16) |
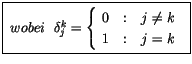 |
|
|
(2.17) |
Tauscht man die obere und untere Indizes in (2.17), so findet man:
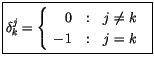 |
|
|
(2.18) |
Die Matrixschreibweise des Tensorquadrats lautet:
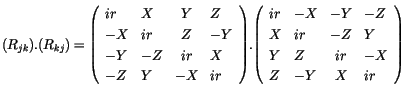 |
|
|
(2.19) |
Nach (2.16) lassen sich das Produkt zweier Vierertensoren auf das Produkt zweier
Vierervektoren zurückführen. So lassen sich die Vierertensoren quadrieren;
das Quadrat eines Vierertensors wird auf das Quadrat eines Vierervektors
zurückgeführt. Für das Quadrat eines Vierervektors der Impulstheorie
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ (R_j)^2 = R^2 \ - \ c^2T^2 \ $}$](IMG54.GIF) |
|
|
(2.20) |
Analog zu (2.16),.., (2.19) finden wir für die Energietheorie
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ x^{jk} \ . \ x^{kj} = {\delta}_j^k...
...j)^2 \ \ , \ \ {\delta}_j^k = die \ \ Einheitstensor \index{Einheitstensor}\ $}$](IMG55.GIF) |
|
|
(2.21) |
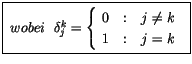 |
|
|
(2.22) |
Beim Vertauschen der oberen und unteren Indizes in (2.22) findet man:
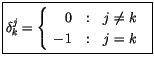 |
|
|
(2.23) |
Die Matrixdarstellung des Tensorquadrats der Energietheorie
lautet:
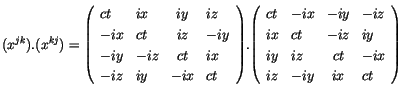 |
|
|
(2.24) |
Analog zu (2.20) in der Impulstheorie
ist das Quadrat des Viererortsvektors
der Energietheorie:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ (x^j)^2 = c^2t^2 \ - \ r^2 \ $}$](IMG57.GIF) |
|
|
(2.25) |




Nächste Seite: Der Abstand
Aufwärts: Spiegelung der Vektoren
Vorherige Seite: Spiegelung der Vektoren
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ R_{jk} \ . \ R_{kj} = \delta_j^k \ . \ (R_j)^2 \ \ , \ \ \delta_j^k = die \ \ Einheitstensor \ $}$](IMG50.GIF)
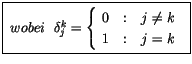
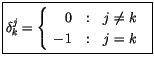
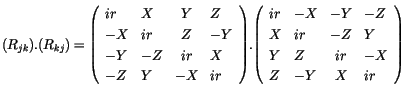
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ (R_j)^2 = R^2 \ - \ c^2T^2 \ $}$](IMG54.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ x^{jk} \ . \ x^{kj} = {\delta}_j^k...
...j)^2 \ \ , \ \ {\delta}_j^k = die \ \ Einheitstensor \index{Einheitstensor}\ $}$](IMG55.GIF)
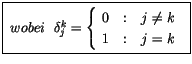
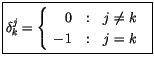
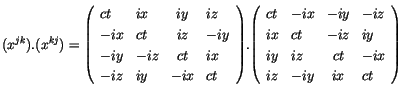
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ (x^j)^2 = c^2t^2 \ - \ r^2 \ $}$](IMG57.GIF)