



Nächste Seite: Das Atom
Aufwärts: Die Eigenwerte der Kugelfunktionen
Vorherige Seite: Die Eigenwerte der Kugelfunktionen
Inhalt
Index
Der Rotator in der ET
Wir ermitteln nun die Eigenwerte von
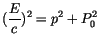 in der Differentialgleichung (10.3). Zuerst separieren wir die Funktion
in der Differentialgleichung (10.3). Zuerst separieren wir die Funktion 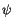
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi \ = \ \psi_0 \ {\sf exp} \left\...
...isplaystyle\frac {\, p_{(\varphi)}r\, sin(\vartheta)\varphi }{\hbar}\right\} $}$](IMG752.GIF) |
|
|
(10.38) |
und setzen
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi \ = \ R_{(r)} \ . \ \theta_{(\vartheta)} \ . \ \phi_{(\varphi)} \qquad $}$](IMG753.GIF) |
|
|
(10.39) |
Für den periodischen Exponent von
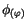 schreiben wir:
schreiben wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p_{(\varphi)} \, r\, sin(\vartheta) \ = \ m\, \hbar \quad \quad $}$](IMG755.GIF) |
|
|
(10.40) |
für
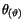
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p_{(\vartheta)} \, r \ = \ s \, \hbar \quad \quad $}$](IMG757.GIF) |
|
|
(10.41) |
und für 
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p_{(r)} \, r \, \ = \ j\, \hbar \quad \quad \quad $}$](IMG759.GIF) |
|
|
(10.42) |
Wir führen eine zweite Variabel 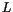 ein und schreiben vorerst für
ein und schreiben vorerst für 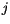 und
und 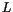
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}j \, = \, (l\, + \, s) \quad \quad $...
...}L= \, \sqrt{\, ls \, - (\displaystyle\frac {s^2}{2})\,\,} \quad \quad \quad $}$](IMG762.GIF) |
|
|
(10.43) |
Wobei 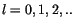 ganze Zahl,
ganze Zahl,
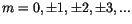 ebenfalls ganze Zahl
und
ebenfalls ganze Zahl
und
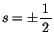 ist.
Der radiale Anteil der Wellengleichung ist unabhängig von
den
ist.
Der radiale Anteil der Wellengleichung ist unabhängig von
den 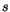 bzw.
bzw. 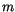 Werten, aber wohl abhängig von dem gemischten
Produkt
Werten, aber wohl abhängig von dem gemischten
Produkt 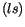 .
Die rechte Seite von (10.3) ist proportional zu
.
Die rechte Seite von (10.3) ist proportional zu
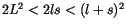 .
Ähnlich wie in IT wird hier der Term
.
Ähnlich wie in IT wird hier der Term 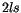 auf den
radialen Anteil symetrisch verteilt. Zu radialem Anteil
auf den
radialen Anteil symetrisch verteilt. Zu radialem Anteil
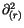 entfällt der Beitrag
entfällt der Beitrag 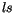 .
Für
.
Für 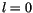 wird
wird 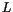 imaginär und damit ein Hinweis, daß dieser L-Wert
einer Erhaltungsgröße der IT ist. Außerdem ist Dieses
imaginär und damit ein Hinweis, daß dieser L-Wert
einer Erhaltungsgröße der IT ist. Außerdem ist Dieses 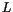 -Term eine
notwendige Bedingung für ein gebundenes Teilchen.
Der Eigenwert dieser Differentialgleichung hat bei
-Term eine
notwendige Bedingung für ein gebundenes Teilchen.
Der Eigenwert dieser Differentialgleichung hat bei 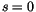 sein
Minimum und führt zu den sogenannten
Rotator Gleichungen. Für die drei Funktionen
sein
Minimum und führt zu den sogenannten
Rotator Gleichungen. Für die drei Funktionen
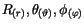 in (10.39)
erhalten wir:
in (10.39)
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{(r)} = \ \psi_0 \, {\bf exp}\left...
...{und} \ \theta_{(\vartheta)} = \ {\sf exp}\left\{ - s \, \vartheta\right\} \ $}$](IMG771.GIF) |
|
|
(10.44) |
Mit (10.40), (10.41) und (10.42) schreiben wir die rechte Seite von (10.3) um und erhalten
jeweils für
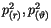 und
und
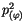 :
:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p^2_{(r)}= \, (\, sl\, - \, \display...
...= \, (\, m^2\, )\, \displaystyle\frac {\hbar^2}{r^2\, sin(\vartheta)^2}\quad $}$](IMG774.GIF) |
|
|
(10.45) |
Da wir uns für die Eigenwerte des Eigendrehimpulses interessieren, ist
der radiale Anteil der Wellengleichung (10.37) gleich Null zu setzen 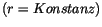 .
Mit (10.37)
und
.
Mit (10.37)
und 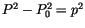 schreiben wir (9.3) um und erhalten wir die Differentialgleichung der
Kugelfunktionen:
schreiben wir (9.3) um und erhalten wir die Differentialgleichung der
Kugelfunktionen:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar^2 \displaystyle\frac {1}{sin(\...
...tial \varphi})^2 \psi + p^2\psi = 2\, (p_{(\vartheta,\varphi)})^2 \psi \quad $}$](IMG777.GIF) |
|
|
(10.46) |
Da 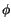 in (10.46) nicht explizite vorkommt, kann man den
in (10.46) nicht explizite vorkommt, kann man den 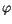 abhängigen Differntialterm integrieren.
Die
abhängigen Differntialterm integrieren.
Die
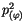 Komponente rechnen wir mit Hilfe von (10.40)
um und bringen sie schließlich auf die linke Seite
Komponente rechnen wir mit Hilfe von (10.40)
um und bringen sie schließlich auf die linke Seite
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar^2 \displaystyle\frac {1}{sin(\...
...c {m^2}{r^2\, sin(\vartheta)^2}\, ) \theta \ = \ 2 \, (p_\vartheta)^2 \theta $}$](IMG779.GIF) |
|
|
(10.47) |
Der Eigenwert dieser Differentialgleichung hat für
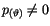 einen
optimalen Wert.
einen
optimalen Wert.
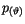 findet man äquivalent zu
findet man äquivalent zu 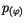 aus der
Beziehung:
aus der
Beziehung:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}2\, (p_\vartheta)^2 \ = \ s^2\, \displaystyle\frac {\hbar^2}{\, r^2\, } \quad \quad $}$](IMG783.GIF) |
|
|
(10.48) |
Setezn wir (10.48) in der linken Seite von (10.47) ein und multiplizieren wir
diese Gleichung mit
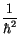 , so können wir für seinen Eigenwert
, so können wir für seinen Eigenwert 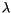 schreiben:
schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \displaystyle\frac {\, p^2}{\...
...rac {s^2}{r^2}\, \right) \ = \ \displaystyle\frac {\lambda}{r^2} \quad \quad $}$](IMG784.GIF) |
|
|
(10.49) |
und damit geht (10.47) über in
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {1}{sin(\vartheta...
... \ \displaystyle\frac {m^2}{r^2\, sin(\vartheta)^2}\, ) \theta \ = \ 0 \quad $}$](IMG785.GIF) |
|
|
(10.50) |
Wir führen 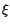 als unabhängige Variabel ein und betrachten
als unabhängige Variabel ein und betrachten 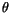 als Funktion von
als Funktion von 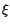
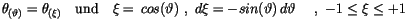 |
|
|
(10.51) |
dann wird aus (10.50)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(1\, - \, \xi^2)\theta'' \, - \, 2\x...
... \, \displaystyle\frac {m^2}{(1\, - \, \xi^2)}\, \right)\theta \ = \ 0 \quad $}$](IMG788.GIF) |
|
|
(10.52) |
Wir untersuchen nun das Verhalten der Lösung von 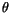 in der Nähe der
singulären Punkte
in der Nähe der
singulären Punkte 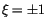 . Wir führen die neuen Variable
. Wir führen die neuen Variable 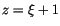 und
und
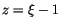 ein und wenden uns zuerst dem Punkt
ein und wenden uns zuerst dem Punkt 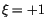 zu und erhalten:
zu und erhalten:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\theta''\, + \, \displaystyle\frac {...
...\, + \, \displaystyle\frac {m^2}{(z)^2\, (2+z)^2}\, \right)\, \theta \ = \ 0 $}$](IMG793.GIF) |
|
|
(10.53) |
Zur Lösung dieser Differentialgleichung setzen wir 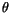 in Form einer
Potenzreihe ein. Wobei sich
in Form einer
Potenzreihe ein. Wobei sich 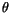 partial aus
partial aus 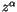 und die Reihe
und die Reihe 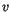 zusammensetzt.
zusammensetzt.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\theta= \, (\, z^{\alpha} \, )\, v \ \ \ , \ v= a_0+a_1\, z+a_2\, z^2+...+a_\nu\, z^\nu +..\ $}$](IMG795.GIF) |
|
|
(10.54) |
Bei der Bestimmung der charkteristischen Gleichung geht die Potenzreihe 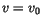 in den Berechnungen ein
in den Berechnungen ein 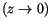 . Tragen wir (10.54) in der linken Seite von
(10.53) ein und bilden den Faktor von
. Tragen wir (10.54) in der linken Seite von
(10.53) ein und bilden den Faktor von 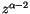 , so finden
wir:
, so finden
wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, \alpha(\alpha\, - \, 1) \, + \, \alpha \, - \, \displaystyle\frac {m^2}{4}\, \right) \, a_0 \ = \ 0 \quad $}$](IMG799.GIF) |
|
|
(10.55) |
Für 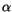 erhalten wir:
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\alpha = \ \pm \displaystyle\frac {m}{2} \quad\quad\quad $}$](IMG669.GIF) |
|
|
(10.56) |
Den gleichen Wert für 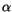 erhält man, falls man sich dem zweiten singulären
Punkt
erhält man, falls man sich dem zweiten singulären
Punkt 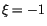 zuwendet. Da die Lösung unseres Problems endlich sein soll,
wählen wir das positive Vorzeichen
zuwendet. Da die Lösung unseres Problems endlich sein soll,
wählen wir das positive Vorzeichen
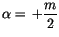 . Nun können
wir (10.54) wie folgt darstellen:
. Nun können
wir (10.54) wie folgt darstellen:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\theta= \, (\, 1\, - \, \xi^2\, )^{\displaystyle\frac {m}{2}} \, \ v \quad $}$](IMG801.GIF) |
|
|
(10.57) |
wobei 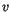 jetzt zweckmäßigerweise eine Potenzreihe von
jetzt zweckmäßigerweise eine Potenzreihe von 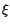 und nicht mehr von
und nicht mehr von
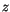 zu nehmen ist.
zu nehmen ist.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}v \, = \, \sum\limits_{\nu = 0}^{\infty}\, a_\nu \, \xi^\nu \quad \quad \quad $}$](IMG803.GIF) |
|
|
(10.58) |
Setzen wir (10.57) in (10.52) ein, so finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(1\, -\, \xi^2)\, v'' \, - \, 2(m\, + \, 1)\, \xi\, v' \, + \, (\lambda \, - \, m \, - \, m^2)\, v \ = \ 0 \quad $}$](IMG804.GIF) |
|
|
(10.59) |
Die Integration dieser Gleichung erfolgt mittels Potenzreihe (10.58). Nach
Eintragen in die Differentialgleichung erhalten wir die Rekursionsformel zur
Bestimmung der Koeffizienten 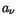 .
.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}((\nu\, + \, 2)\, (\nu\, + \, 1))\ a...
..., + \, 2(m \, + \, 1)\, \nu \, - \, \lambda\, + \, m \, + \, m^2\, )\, a_\nu $}$](IMG806.GIF) |
|
|
(10.60) |
Die Reihe (10.58) wird für 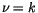 ein Polynom k-ten Grades und somit
verschwinden alle Koeffizienten von
ein Polynom k-ten Grades und somit
verschwinden alle Koeffizienten von 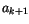 ,
, 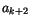 . Die Reihe kann
nur dann abbrechen, falls
. Die Reihe kann
nur dann abbrechen, falls
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ (\, k \, (k \, - \, 1)\, + \, 2(m \, + \, 1)\, k \, - \, \lambda\, + \, m \, + \, m^2\, )\, a_k \ = \ 0 \quad $}$](IMG809.GIF) |
|
|
(10.61) |
gesetzt wird. Daraus folgt:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ \lambda \ = \ (\, k \, + \, m\, )\, (\, k \, + \, m \, + \, 1\, )\, \quad $}$](IMG810.GIF) |
|
|
(10.62) |
setzen wir für 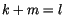 ein, so finden wir für
ein, so finden wir für 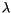 :
:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lambda \ = \ l\, (\, l\, + \, 1\, ) \quad \quad \quad $}$](IMG811.GIF) |
|
|
(10.63) |
Nun können wir für (10.49) schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, \displaystyle\frac {\, E^2}...
...}\, \right) \ = \ \displaystyle\frac {l\, (\, l\, +\, 1\, )}{r^2}\quad \quad $}$](IMG812.GIF) |
|
|
(10.64) |
Da der Spin 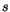 einer Orientierungsquant des nichtpunktförmigen Teilchens
darstellt, setzen wir
einer Orientierungsquant des nichtpunktförmigen Teilchens
darstellt, setzen wir 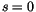 ein und stellen die Gleichung nach
ein und stellen die Gleichung nach
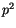 um, so gilt:
um, so gilt:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p^2 \ = \, k^2 \, (\displaystyle\frac {\hbar}{r})^2 \qquad \mbox{mit} \quad k=\sqrt{l(\, l + 1\, )\, }\quad \ $}$](IMG814.GIF) |
|
|
(10.65) |
oder auch
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {\, E\, }{c})^2 \...
... \, \displaystyle\frac {\hbar^2}{r^2} \ + \ (\, m^2_0 \, c^2\, ) \quad \quad $}$](IMG815.GIF) |
|
|
(10.66) |




Nächste Seite: Das Atom
Aufwärts: Die Eigenwerte der Kugelfunktionen
Vorherige Seite: Die Eigenwerte der Kugelfunktionen
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi \ = \ \psi_0 \ {\sf exp} \left\...
...isplaystyle\frac {\, p_{(\varphi)}r\, sin(\vartheta)\varphi }{\hbar}\right\} $}$](IMG752.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi \ = \ \psi_0 \ {\sf exp} \left\...
...isplaystyle\frac {\, p_{(\varphi)}r\, sin(\vartheta)\varphi }{\hbar}\right\} $}$](IMG752.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi \ = \ R_{(r)} \ . \ \theta_{(\vartheta)} \ . \ \phi_{(\varphi)} \qquad $}$](IMG753.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p_{(\varphi)} \, r\, sin(\vartheta) \ = \ m\, \hbar \quad \quad $}$](IMG755.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p_{(\vartheta)} \, r \ = \ s \, \hbar \quad \quad $}$](IMG757.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p_{(r)} \, r \, \ = \ j\, \hbar \quad \quad \quad $}$](IMG759.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}j \, = \, (l\, + \, s) \quad \quad $...
...}L= \, \sqrt{\, ls \, - (\displaystyle\frac {s^2}{2})\,\,} \quad \quad \quad $}$](IMG762.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{(r)} = \ \psi_0 \, {\bf exp}\left...
...{und} \ \theta_{(\vartheta)} = \ {\sf exp}\left\{ - s \, \vartheta\right\} \ $}$](IMG771.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p^2_{(r)}= \, (\, sl\, - \, \display...
...= \, (\, m^2\, )\, \displaystyle\frac {\hbar^2}{r^2\, sin(\vartheta)^2}\quad $}$](IMG774.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar^2 \displaystyle\frac {1}{sin(\...
...tial \varphi})^2 \psi + p^2\psi = 2\, (p_{(\vartheta,\varphi)})^2 \psi \quad $}$](IMG777.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar^2 \displaystyle\frac {1}{sin(\...
...c {m^2}{r^2\, sin(\vartheta)^2}\, ) \theta \ = \ 2 \, (p_\vartheta)^2 \theta $}$](IMG779.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}2\, (p_\vartheta)^2 \ = \ s^2\, \displaystyle\frac {\hbar^2}{\, r^2\, } \quad \quad $}$](IMG783.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \displaystyle\frac {\, p^2}{\...
...rac {s^2}{r^2}\, \right) \ = \ \displaystyle\frac {\lambda}{r^2} \quad \quad $}$](IMG784.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {1}{sin(\vartheta...
... \ \displaystyle\frac {m^2}{r^2\, sin(\vartheta)^2}\, ) \theta \ = \ 0 \quad $}$](IMG785.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(1\, - \, \xi^2)\theta'' \, - \, 2\x...
... \, \displaystyle\frac {m^2}{(1\, - \, \xi^2)}\, \right)\theta \ = \ 0 \quad $}$](IMG788.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\theta''\, + \, \displaystyle\frac {...
...\, + \, \displaystyle\frac {m^2}{(z)^2\, (2+z)^2}\, \right)\, \theta \ = \ 0 $}$](IMG793.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\theta= \, (\, z^{\alpha} \, )\, v \ \ \ , \ v= a_0+a_1\, z+a_2\, z^2+...+a_\nu\, z^\nu +..\ $}$](IMG795.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, \alpha(\alpha\, - \, 1) \, + \, \alpha \, - \, \displaystyle\frac {m^2}{4}\, \right) \, a_0 \ = \ 0 \quad $}$](IMG799.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\alpha = \ \pm \displaystyle\frac {m}{2} \quad\quad\quad $}$](IMG669.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\theta= \, (\, 1\, - \, \xi^2\, )^{\displaystyle\frac {m}{2}} \, \ v \quad $}$](IMG801.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}v \, = \, \sum\limits_{\nu = 0}^{\infty}\, a_\nu \, \xi^\nu \quad \quad \quad $}$](IMG803.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(1\, -\, \xi^2)\, v'' \, - \, 2(m\, + \, 1)\, \xi\, v' \, + \, (\lambda \, - \, m \, - \, m^2)\, v \ = \ 0 \quad $}$](IMG804.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}((\nu\, + \, 2)\, (\nu\, + \, 1))\ a...
..., + \, 2(m \, + \, 1)\, \nu \, - \, \lambda\, + \, m \, + \, m^2\, )\, a_\nu $}$](IMG806.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ (\, k \, (k \, - \, 1)\, + \, 2(m \, + \, 1)\, k \, - \, \lambda\, + \, m \, + \, m^2\, )\, a_k \ = \ 0 \quad $}$](IMG809.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ \lambda \ = \ (\, k \, + \, m\, )\, (\, k \, + \, m \, + \, 1\, )\, \quad $}$](IMG810.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lambda \ = \ l\, (\, l\, + \, 1\, ) \quad \quad \quad $}$](IMG811.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, \displaystyle\frac {\, E^2}...
...}\, \right) \ = \ \displaystyle\frac {l\, (\, l\, +\, 1\, )}{r^2}\quad \quad $}$](IMG812.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}p^2 \ = \, k^2 \, (\displaystyle\frac {\hbar}{r})^2 \qquad \mbox{mit} \quad k=\sqrt{l(\, l + 1\, )\, }\quad \ $}$](IMG814.GIF)
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {\, E\, }{c})^2 \...
... \, \displaystyle\frac {\hbar^2}{r^2} \ + \ (\, m^2_0 \, c^2\, ) \quad \quad $}$](IMG815.GIF)