



Nächste Seite: Das positive, negative und
Aufwärts: Das duale Wirkungsintegral
Vorherige Seite: Die Wirkung in allgemeinen
Inhalt
Index
Der Gültigkeitsbereich der Wellenfunktion soll die dualen Grenzen von
Compton bis De Broglie Wellenlänge erfassen. Die Bedingung
hierfür ist das Berücksichtigen der zweifachen Wirkungsgröße 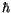 in dem Argument der Wellenfunktion.
Außerdem muß das Argument der Wellenfunktion den Förderungen der Eindeutigkeit
(1 Teilchen-System) Rechnung tragen. Nach Gesetzen der
Wahrscheinlichkeitstheorie ist die
Wahrscheinlichkeit, das Teilchen im Zeitpunkt T/t im Volumen V/v zu finden
durch die Beziehung:
in dem Argument der Wellenfunktion.
Außerdem muß das Argument der Wellenfunktion den Förderungen der Eindeutigkeit
(1 Teilchen-System) Rechnung tragen. Nach Gesetzen der
Wahrscheinlichkeitstheorie ist die
Wahrscheinlichkeit, das Teilchen im Zeitpunkt T/t im Volumen V/v zu finden
durch die Beziehung:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits \Psi^2 \, dV \ = \ 1 \quad \quad$}\quad
\mbox{\bf Die Impulstheorie}$](IMG322.GIF) |
|
|
(4.68) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits \psi^2 \, dv \ = \ 1 \quad \quad $}\quad
\mbox{\bf Die Energietheorie}$](IMG323.GIF) |
|
|
(4.69) |
gegeben. Die Größe 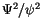 nennen wir die
Wahrscheinlichkeitsdichte der dualen Physik,
die wir mit der
Bezeichnung
nennen wir die
Wahrscheinlichkeitsdichte der dualen Physik,
die wir mit der
Bezeichnung
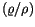 für die Dichte versehen werden. Für die Impulstheorie
erhalten wir:
für die Dichte versehen werden. Für die Impulstheorie
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\varrho^-}_{(cT,\vec{R})}\ = \ {\va...
...\{ \displaystyle\frac { P \ cT \ - \ \vec{P} . \vec{R} }{\hbar} \right\} \ \ $}$](IMG326.GIF) |
|
|
(4.70) |
Analog finden wir für die Energietheorie:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\rho^+}_{(ct,\vec{r})}\ = \ {\rho^-...
...\{ \displaystyle\frac { p \ ct \ - \ \vec{p} . \vec{r} }{\hbar} \right\} \ \ $}$](IMG327.GIF) |
|
|
(4.71) |
Analoge Beziehungen gelten für das positive Elementar-Teilchen.




Nächste Seite: Das positive, negative und
Aufwärts: Das duale Wirkungsintegral
Vorherige Seite: Die Wirkung in allgemeinen
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits \Psi^2 \, dV \ = \ 1 \quad \quad$}\quad
\mbox{\bf Die Impulstheorie}$](IMG322.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits \Psi^2 \, dV \ = \ 1 \quad \quad$}\quad
\mbox{\bf Die Impulstheorie}$](IMG322.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits \psi^2 \, dv \ = \ 1 \quad \quad $}\quad
\mbox{\bf Die Energietheorie}$](IMG323.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\varrho^-}_{(cT,\vec{R})}\ = \ {\va...
...\{ \displaystyle\frac { P \ cT \ - \ \vec{P} . \vec{R} }{\hbar} \right\} \ \ $}$](IMG326.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\rho^+}_{(ct,\vec{r})}\ = \ {\rho^-...
...\{ \displaystyle\frac { p \ ct \ - \ \vec{p} . \vec{r} }{\hbar} \right\} \ \ $}$](IMG327.GIF)