



Nächste Seite: Das Feld in der
Aufwärts: Die 4. Teilchen-Gleichungen der
Vorherige Seite: Die Erhaltung des Viererpotentials
Inhalt
Index
Die Erhaltung der Elementarladung
Um die Integralform
des Viererpotentials der Impulstheorie zu finden,
errechnen wir das Produkt
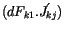 auf der rechten Seite
von (6.24) aus. Unter der Berücksichtigung der Beziehung in (6.29) und
Vernachlässigen der Glieder, des starken Wechselwirkungspotentials und des
magnetischen Potentials des Elektrons finden wir:
auf der rechten Seite
von (6.24) aus. Unter der Berücksichtigung der Beziehung in (6.29) und
Vernachlässigen der Glieder, des starken Wechselwirkungspotentials und des
magnetischen Potentials des Elektrons finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\begin{array}{rcl}\alpha \left(i (\d...
...\displaystyle\frac {{\vec{J}^+}_{(cT,\vec{R})}}{c \ \ R}) \right)\end{array} $}$](IMG436.GIF) |
|
|
(6.30) |
Die Erhaltungsgrößen in der Gleichung (6.30) sind die zeitlosen
Integranden,die wir hier besonders unterstreichen möchten. Für die komponenten
des Viererpotentials erhalten wir schließlich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_{k1} \ = \ \displaystyle\frac {1}{...
... -\displaystyle\frac {{\vec{J}^+}_{(cT,\vec{R})}}{c \ \ R}\Big) \ dV \ \quad $}$](IMG437.GIF) |
|
|
(6.31) |
Sie ist die Lösung der Gleichung (6.1). Damit ist unsere Behauptung nämlich
die Erhaltung des Viererpotentials erwiesen.
Wir werden nun einer weiteren Behauptung, nämlich (6.23) die räumliche
Verteilung
der Elementarladung 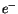 nachgehen und sie ebenfalls beweisen. Die Beziehung für stationären Zustand
nachgehen und sie ebenfalls beweisen. Die Beziehung für stationären Zustand
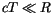
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits_V \ dV \ {...
...{ \displaystyle\frac { - \vec{P} \ . \ \vec{R} }{\hbar} \right\} \ = \ e^- \ $}$](IMG439.GIF) |
|
|
(6.32) |
wandeln wir zuerst in Kugelkoordinaten um. Für das Skalarprodukt
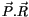 schreiben wir
schreiben wir
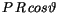 und setzen (-
und setzen (-
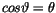 ) ein. Weiterhin
berücksichtigen wir, daß für die Beziehung
) ein. Weiterhin
berücksichtigen wir, daß für die Beziehung
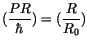 gilt, so erhalten wir:
gilt, so erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits_{R=0}^{\in...
...exp}\left\{\displaystyle\frac {R}{R_0} \ \theta\right\} d \theta \ = \ e^- \ $}$](IMG444.GIF) |
|
|
(6.33) |
Nach eliminieren von 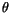 erhalten wir:
erhalten wir:
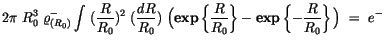 |
|
|
(6.34) |
oder mit der Substitution
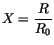 finden wir:
finden wir:
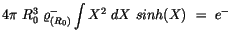 |
|
|
(6.35) |
Nach Integration dieser Gleichung erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varrho^-_{(R_0)} \ = \ \left(\displ...
...\ (\, X^2\, + \, 2\, ) cosh(X) - 2X \, sinh(X) \, - \, 2 \right)}^{-1} \quad $}$](IMG449.GIF) |
|
|
(6.36) |
In der ersten Klammer erkennt man die Flächendichte der Implulstheorie. Für
den äußersten Rand der Oberfläche 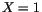 finden wir:
finden wir:
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\varrho^-_{(R_0)} \ = \ \left(\displa...
..., + \, \displaystyle\frac {{\bf exp}\{1\}}{2}\, - \, 2 \, \right)^{-1} \quad $}$](IMG451.GIF) |
|
|
(6.37) |




Nächste Seite: Das Feld in der
Aufwärts: Die 4. Teilchen-Gleichungen der
Vorherige Seite: Die Erhaltung des Viererpotentials
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\begin{array}{rcl}\alpha \left(i (\d...
...\displaystyle\frac {{\vec{J}^+}_{(cT,\vec{R})}}{c \ \ R}) \right)\end{array} $}$](IMG436.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\begin{array}{rcl}\alpha \left(i (\d...
...\displaystyle\frac {{\vec{J}^+}_{(cT,\vec{R})}}{c \ \ R}) \right)\end{array} $}$](IMG436.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_{k1} \ = \ \displaystyle\frac {1}{...
... -\displaystyle\frac {{\vec{J}^+}_{(cT,\vec{R})}}{c \ \ R}\Big) \ dV \ \quad $}$](IMG437.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits_V \ dV \ {...
...{ \displaystyle\frac { - \vec{P} \ . \ \vec{R} }{\hbar} \right\} \ = \ e^- \ $}$](IMG439.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\int \limits_{R=0}^{\in...
...exp}\left\{\displaystyle\frac {R}{R_0} \ \theta\right\} d \theta \ = \ e^- \ $}$](IMG444.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varrho^-_{(R_0)} \ = \ \left(\displ...
...\ (\, X^2\, + \, 2\, ) cosh(X) - 2X \, sinh(X) \, - \, 2 \right)}^{-1} \quad $}$](IMG449.GIF)
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\varrho^-_{(R_0)} \ = \ \left(\displa...
..., + \, \displaystyle\frac {{\bf exp}\{1\}}{2}\, - \, 2 \, \right)^{-1} \quad $}$](IMG451.GIF)