



Nächste Seite: Partielle Differentiale 2. Ordnung
Aufwärts: Die Differentiale erste und
Vorherige Seite: Partielle Differentiale 2. Ordnung
Inhalt
Index
Der Quotient aus den infinitesimalen Vierergeschwindigkeitsvektoren und dem
skalaren Abstand bilden die Ableitungen, die wir hier mit den Komponenten der
Viererbeschleunigungstensor
der Energietheorie bezeichnen.
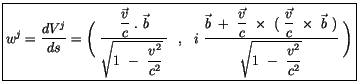 |
|
|
(2.73) |
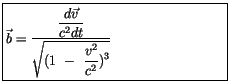 |
|
|
(2.74) |
Mit (2.59) erhalten wir für das doppelte Kreuzprodukt des imaginären
Zählers in (2.73) :
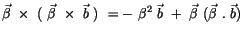 |
|
|
(2.75) |
Steht der Geschwindigkeitsvektor 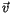 senkrecht auf dem
Beschleunigungsvektor
senkrecht auf dem
Beschleunigungsvektor 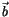 , so verschwindet
das Skalarprodukt in der Klammer. Im Gegensatz zu der Impulstheorie
verschwindet nicht der imaginäre Teil dieses Vierervektors. Durch das Differenzieren vom Quadrat des
Vierergeschwindigkeitstensors (2.55) erhält man:
, so verschwindet
das Skalarprodukt in der Klammer. Im Gegensatz zu der Impulstheorie
verschwindet nicht der imaginäre Teil dieses Vierervektors. Durch das Differenzieren vom Quadrat des
Vierergeschwindigkeitstensors (2.55) erhält man:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V^{jk} \ . \ w^{kj} \ + \ w^{jk} \ . \ V^{kj} \ = \ N_{jk} \ = \ N_{kj} $}$](IMG156.GIF) |
|
|
(2.76) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V^{jk} \ . \ w^{kj} \ = \ - w^{jk} \ . \ V^{kj} $}$](IMG157.GIF) |
|
|
(2.77) |




Nächste Seite: Partielle Differentiale 2. Ordnung
Aufwärts: Die Differentiale erste und
Vorherige Seite: Partielle Differentiale 2. Ordnung
Inhalt
Index
root
1999-07-07
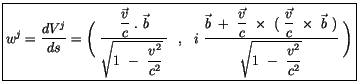
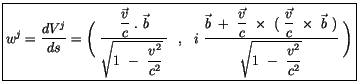
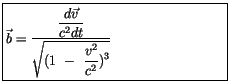
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V^{jk} \ . \ w^{kj} \ + \ w^{jk} \ . \ V^{kj} \ = \ N_{jk} \ = \ N_{kj} $}$](IMG156.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V^{jk} \ . \ w^{kj} \ = \ - w^{jk} \ . \ V^{kj} $}$](IMG157.GIF)